Research Summary

Prof. Suresh is the director of the Engineering Representations and Simulation Lab (ERSL) . The ERSL research group focuses on large-scale topology optimization, design for additive manufacturing, and high performance finite element analysis (FEA).

The novelty in the topology optimization approach is the concept of topological level-set that combines topological sensitivity and level-set in a simple and robust manner. This has resulted in innovative methods for handling manufacturing constraints, tracing Pareto curves in multi-objective optimization, designing multi-materials and compliant mechanisms.

In parallel, the research group has made several ground breaking advances in high-performance finite element analysis. The dual-representation strategy demonstrated how classic beam and shell theories can be used as efficient preconditioners for 3D FEA. The novel concept of tangled FEA extends classic FEA to tangled meshes containing inverted elements, bypassing the unsolved problem of mesh untangling. The group also proposed the idea of limited-memory deflated FEA to exploit modern multi-core CPUs and many-core graphic programmable units (GPUs).

Research Interests

  • Large-scale multi-constrained topology optimization
  • Design optimization for additive manufacturing
  • Additive manufacturing simulation
  • High-performance (GPU/Cloud) computing
  • Limited-memory finite element analysis
  • Mesh generation

Software

Several software modules have been created by our research group; please see links to the right.

For example, a Matlab-based design optimization toolbox Design Optimization Software accompanies the text Design Optimization using Matlab and SolidWorks, authored by Prof. Krishnan Suresh. This module also includes SolidLab, a Matlab-based interface to SolidWorks. Also available is a Matlab-based Medial Axis Generator (Matlab) for 2D objects.

A Matlab-based design reliabiity software toobox Design Reliability Software has also been recently added.

In classic NURBS, the weights are equal along all physical coordinates. By allowing the weights to change independently in each physical coordinate, a new curve is generated which is called Generalized NURBS (GNURBS). GNURBS Lab is a MATLAB toolbox devised to generate and manipulate Generalized NURBS curves.

A unique characteristic of the research is that it has been translated into industry-strength software. For example, in 2013, the group released ParetoWorks , a topology optimization software that is integrated into SolidWorks™. It is now used by over 50+ universities around the world, and by several industrial partners. Then, in 2015, the group launched CloudTopopt , a unique cloud-based finite element analysis and topology optimization software, used by several hundred designers around the world.

As part of an outreach activitiy, we have also developed CADjs , a Javascript-based CAD programming environment. CADjs is now used both in undergraduate classes, and at local Middle and High Schools.

Software Links

Current and Graduated ERSL Students

Praveen Yadav

PhD, 2016

CTO, SciArt

praveen.yadav@sciartsoft.com

Shiguang Deng

PhD, 2016

Research Scientist, MSC Software

sdeng9@wisc.edu

Chaman S. Verma

PhD, 2017

Research Scientist, Palo Alto Research Center

chaman.verma@parc.com

Amir M. Mirzendehdel

PhD, 2017

Research Scientist, Palo Alto Research Center

amirzend@parc.com

Alireza Taheri

PhD, 2021

Postdoc, USC

al.h.taheri@gmail.com

Tej Kumar

PhD, 2021

Parametric Technology

tkumar3@wisc.edu

Buzz Rankouhi

PhD Candidate

rankouhi@wisc.edu

Subodh Subedi

PhD Candidate

scsubedi@wisc.edu

Aaditya Chandrasekhar

PhD Candidate

achandrasek3@wisc.edu

Bhaghyashree Prabhune

PhD Candidate

bprabhune@wisc.edu

Saketh Sridhara

PhD Candidate

ssridhara@wisc.edu

Rahul Padhy

MS/PhD Candidate

rkpadhy@wisc.edu

Akshay Kumar

MS/PhD Candidate

akshaykumar@wisc.edu

Anirudh Krishnakumar

MS, 2016

Product Manager GrabCAD

anirudh@grabcad.com

Anirban Niyogi

MS, 2015

niyogi@wisc.edu

Cameron Gilanshah

MS, 2016

gilanshah@uwalumni.com

Victor Cavalcanti

MS, 2015

cavalcanti@wisc.edu

Nikhil Agarwal

Undergrad Research Assistant

nagarwal22@wisc.edu

Alex Buehler

Undergrad Research Assistant

aebuehler@wisc.edu

Jimmy Herman

Undergrad Research Assistant

jherman3@wisc.edu

Victor Markus

Undergrad Research Assistant

vmarkus@wisc.edu

The research group current consists of about 15 highly talented students. Students join ERSL from all over the world including the United States, China, India, Iran, Israel and Europe.

Current Research Projects

  • image
    Topology optimized design for the classic MBB problem.

    Topology optimization benchmark studies

    This is an effort to provide the community with topology optimized models that can be used for 3D-printing, recovery of CAD models, etc. Click here for TO benchMark models

  • image
    A "Thomas Train" structural problem with 50 million degree of freedom solved on a GPU in 24 minutes.

    Limited Memory Deflated Finite Element Analysis

    Large-scale FEA problems with millions of degrees of freedom are becoming commonplace in solid mechanics. The bottleneck in such problems is memory access. The objective of this project is to exploit assembly-free deflation techniques to accelerate FEA.

  • image
    Transient response of a million degree of freedom "Arduino Board" subject to an impulse loading.

    Large-Scale Implicit Structural Dynamics

    The primary computational bottle-neck in implicit structural dynamics is the repeated inversion of the underlying stiffness matrix. A fast inversion technique is proposed by combining the well-known Newmark-beta method, with assembly-free deflated conjugate gradient (AF-DCG) for large-scale problems.

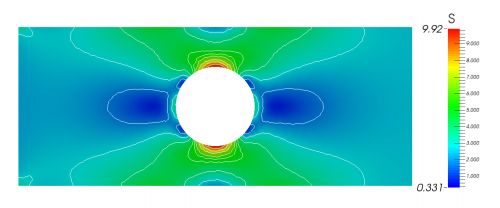
  • image
    A tangled quad mesh over which FEA was solved with high accuracy.

    Finite Element Analysis over a Tangled Mesh

    Classic FEA breaks down if one or more elements gets inverted, i.e., if the mesh gets tangled. But, mesh tangling is unavoidable during mesh generation, mesh morhping and large-scale deformation. The objective of this research is to extend classic FEA to handle tangled meshes.

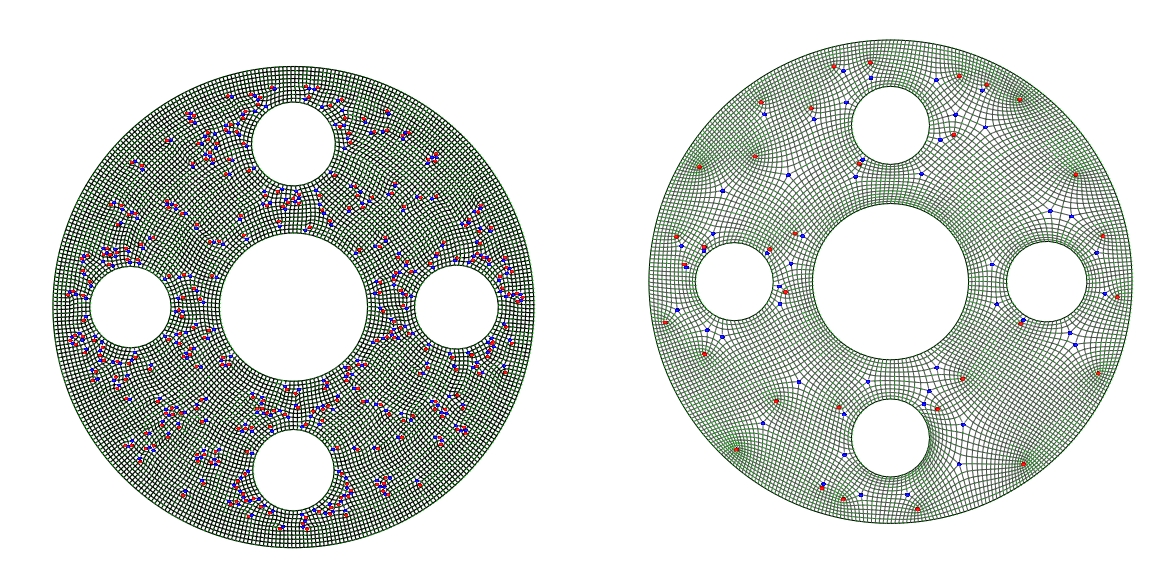
  • image
    The number of singularities in a quad mesh is reduced without affecting element quality.

    Singularity Removal in Quad Meshes

    In quad meshes, nodes connected to exactly 4 quad elements are called regular; otherwise they are referred to as irregular or singular. Singular nodes are detrimental to FEA accuracy. A new singularity removal method has been developed to dramatically reduce the number of node singularities.

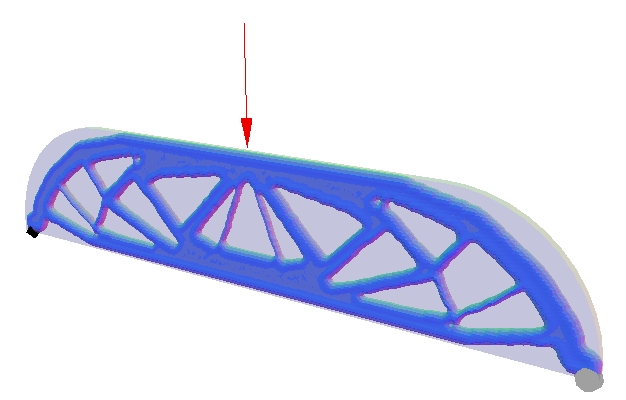
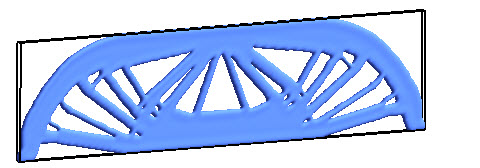
  • image
    The solution to the classic "Michelle Bridge" problem via the topological level-set.

    Topology Optimization via the Topological Level-Set

    The topological level-set method developed by our group directly uses the topological sensitivity field as a level-set for an efficient solution of topology optimization problems.

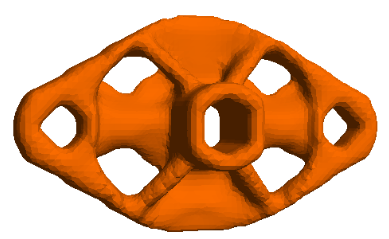
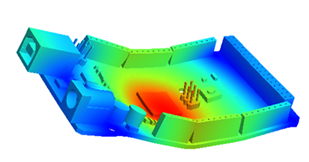
  • image
    Optimal topology of a flange subject to compliance, stress and eigen-value constraints

    Multi-constrained Topology Optimization

    Topology optimization problems subject to several constraints are both theoretically and computationally challenging. The topological level-set method is combined here with augmented Lagrangian methods to solve such multi-constrained topology optimization problems.

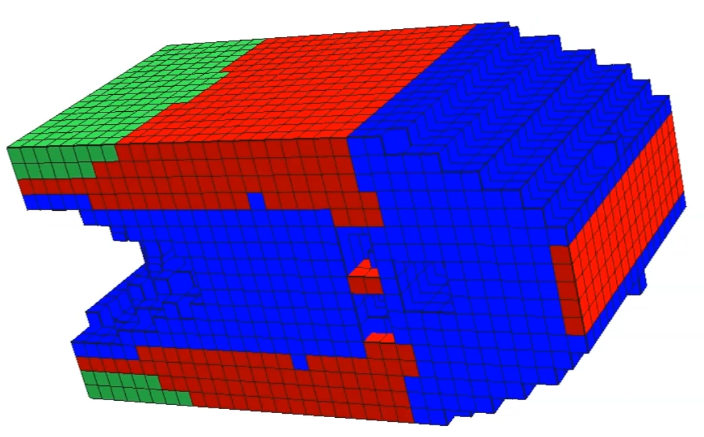
  • image
    The solution to classic cantilever compliance minimization problem, but using three different materials.

    Multi-material Topology Optimization

    As additive manufacturing expands into multi-material, there is a demand for efficient multi-material topology optimization. The classic approach is to impose constraints on the volume-fraction of each of the material constituents. This can artificially restrict the design space. Instead, the total mass and compliance are treated as conflicting objectives, and the corresponding Pareto curve is traced; no additional constraint is imposed on the material composition.

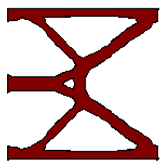
  • image
    A hinge-free solution to the classic cruncher mechanism.

    Hinge-Free Compliant Mechanism Design

    Hinges can lead to high stress concentration in compliant mechanisms. The topological sensitivity concept is exploited here to design hinge-free compliant mechanisms. These mechanisms exhibit high mechanical advantage and low stresses.

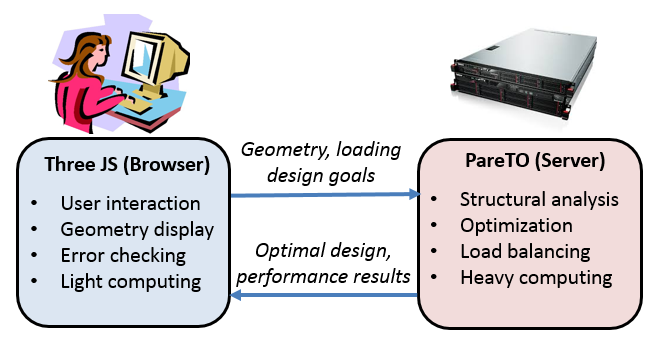
  • image
    Client-server architecture underlying cloudtopopt.

    Topology Optimization on the Cloud

    The wide-spread use of topology optimization has been deterred due to high computational cost and significant software/hardware investment. Our group has developed a cloud based implementation of topology optimization, hosted at www.cloudtopopt.com.

  • image
    A microstructure with optimal bulk modulus.

    Microstructural Optimization

    The objective in microstructural optimization is to find the distribution of one or more 'materials' that would result in a desired microscopic behaviour (ex: negative Poisson ratio). Our group has developed a highly efficient topological sensitivity based method for designing such microstructures and tracing their corresponding Hashin-Shtrikman curves.

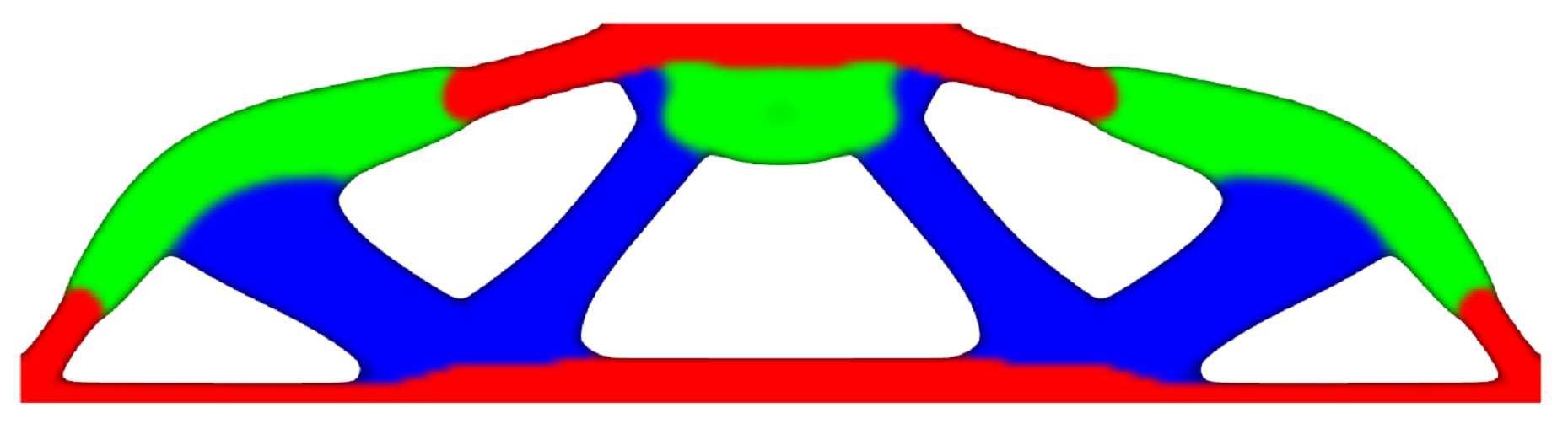
  • image
    A NURBS based iso-geometric solution to the classic MBB problem.

    Iso-Geometric Multi-material Topology Optimization

    The objective here is to exploit the inherent advantages of isogeometric analysis for multi-material topology optimization. Due to the unified parametrization of geometry, analysis and design space, the sensitivities are computed analytically.

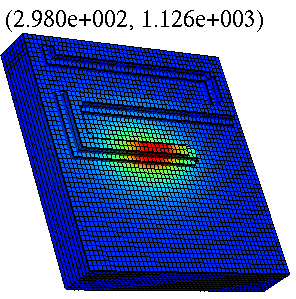
  • image
    A snap-shot of thermo-elastic simulation of the LENS process

    Assembly Free Additive Manufacturing (AM) Simulation

    In AM simulation, repeated meshing and insertion of new elements during material deposition can pose significant implementation challenges. Our group is developing an assembly-free framework for AM simulation that offers several advantages: (1) The workspace is meshed only once at the start of the simulation, (2) addition and deletion of elements is easy since the stiffness matrix is never assembled, and (3) the underlying linear systems of equations can be solved efficiently through assembly-free deflation methods.

Graduated Students

  • 2012 Josh Danczyk (Ph.D.)
  • 2011 Vikalp Mishra (Ph.D.), Inna Turevsky (Ph.D.), Kavous Jorabchi (Ph.D.)
  • 2010 Vaibhav Deshpande (M.S.)
  • 2009 Wa’el Abdel Samad (M.S.)
  • 2008 Sahil Kulakarni (M.S.)
  • 2007 Sankara Hari Gopalakrishnan (M.S)
  • 2006 Himanshu Tiwari (M.S.), Rakesh Vemulapally (M.S.), Murari Sinha (M.S.)
  • 2005 Ameya Sirpotdar (M.S.)

ERSL has graduated 4 PhD and 8 MS students; they are currently employed in academia, as well as semiconductor, machinery and software industries.